[Machine Learning] 과소적합, 과대적합

편향과 분산

직선 모델은 너무 간단해서 복잡한 곡선 관계를 학습하지 못한다는 한계가 있습니다.
모델이 너무 간단해서 데이터의 관계를 잘 학습하지 못하는 경우
그 모델은 편향이 높다 라고 합니다.

모델의 복잡도를 높여서 트레이닝 데이터의 관계를 완벽히 학습했다면
그 모델은 편향이 낮다 라고 할 수 있습니다.

그렇다면, 편향이 낮은 모델은 항상 편향이 높은 모델보다 좋을까요?

꼭 그렇지만은 않습니다.

각 모델이 처음 접하는 데이터인 테스트 데이터 셋에 대해서 모델의 성능을 평가해보면,
트레이닝 데이터의 관계를 완벽하게 나타내는 모델은 너무 트레이닝 데이터에 딱 맞춰서 학습되어있기때문에
처음 보는 테스트 데이터 셋에 대해서는 편향이 높은 모델보다 성능이 더 안좋을 수 있습니다.

이렇게 데이터셋별로 얼마나 일관된 성능을 보여주는지를 분산(Variance)라고 합니다.
다양한 데이터셋 간에 비슷한 성능을 보여주면 분산이 낮다고 하고,
성능 차이가 많이 나면 분산이 높다고 합니다.

위의 경우에는 편향이 너무 낮아 트레이닝 데이터 셋에 너무 딱 맞아 떨어지는 모델은 분산이 높고,
편향이 높은 모델은 분산이 낮다고 말할 수 있습니다.

편향-분산 트레이드오프 (Bias-variance tradeoff)

편향을 높이면 학습이 잘 안되고,
편향이 낮으면 분산이 높아진다고 하고 둘 다 안좋은 것 아닌가..라는 생각이 들 수도 있습니다.

어떻게 해야하는지 설명하기 전에
두 가지 용어만 알아보고 가겠습니다.

과소적합 (underfitting)

과소적합은 모델이 너무 단순해서 데이터의 내재적인 구조를 학습하지 못할 때 발생합니다.

아래 사진과 같은 경우가 과소적합이 일어난 경우라고 할 수 있습니다. 이미지 출처

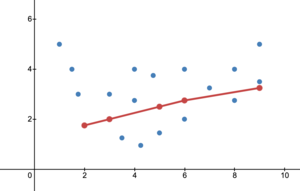
과대적합 (overfitting)

과대적합은 모델이 훈련 데이터에 대해서 너무 잘 맞지만 일반성이 떨어질 때 발생합니다.

아래 사진과 같은 경우가 과대적합이 일어난 경우라고 할 수 있습니다. 이미지 출처

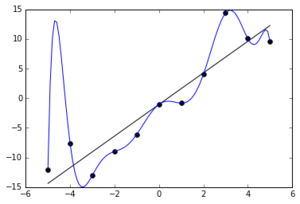
일반적으로 편향과 분산은 하나가 줄어들수록 다른 하나는 늘어나는 경향이 있습니다.
따라서 둘 중 하나를 줄이기 위해서는 다른 하나를 포기해야 하는 관계입니다.
이러한 관계를 편향-분산 트레이드오프 라고 부릅니다.

편향-분산 트레이드오프 문제는 머신 러닝 프로그램들의 성능과 밀접한 관계가 있기 때문에
편향과 분산의 적당한 밸련스를 찾아내야합니다.

위의 과소적합 그래프도, 과대적합 그래프도 아닌
아래와 같은 그래프를 찾아야 한다는 것입니다. 이미지 출처

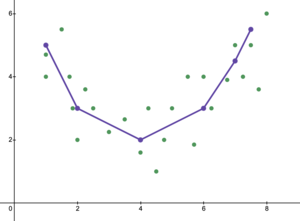
scikit-learn으로 과소적합 방지해보기

우리의 목적은 과소적합도, 과대적합도 되지 않은 모델을 찾는 것입니다.

과소적합은 충분히 복잡한 모델을 쓰는 것으로 간단하게 해결이 가능합니다.
scikit-learn으로 복잡한 회귀 모델을 만들어 과소적합을 한 번 방지해보겠습니다.

정규화 (Regularization)

위의 코드에서 과소적합은 방지됐지만 과대적합이 발생했는데요,
모델 과대적합을 방지해주는 방법 중 하나인 정규화에 대해서 살펴보겠습니다.

과대적합이 되면 가설 함수의 그래프가 데이터에 거의 딱 맞게 그려져서 굴곡이 많고 급격하게 변화하게 됩니다.
함수가 급격하게 변하는 것은 가설 함수의 계수들, 즉 \(\theta\)값이 크기 때문입니다.

정규화는 모델을 학습시킬 때 이 \(\theta\)값들이 너무 커지는 걸 방지하는 방법입니다.
\(\theta\)값들이 너무 커지는 걸 방지하면 트레이닝 데이터에 대한 오차는 조금 커질 수 있어도
위아래로 급격히 변하는 가설 함수를 좀 더 완만하게 만들 수 있습니다.

그렇게 하면 여러 데이터 셋에 대해 좀 더 일관된 성능을 보이기 때문에 과적합을 막을 수 있습니다.

L1, L2 정규화

머신 러닝에서 정규화는 손실 함수에 정규화 항이라는 것을 더해서 \(\theta\)값들이 너무 커지는 것을 방지하는 방법입니다.

여태까지의 좋은 가설 함수를 평가할 때
손실 함수의 아웃풋이 더 작을수록 좋은 가설 함수,
손실 함수의 아웃풋이 클수록 안좋은 가설 함수라고 평가해왔는데요,

과적합을 방지하기 위해서 가설 함수의 평가 기준을 아래와 같이 바꿔주겠습니다.

트레이닝 데이터에 대한 오차도 작고 \(\theta\) 값들도 작아야 좋은 가설 함수이다.

이런 조건을 충족시키기 위한 두 가지 방법을 소개하겠습니다.

L1 정규화

L1 정규화를 적용할 때의 손실 함수의 수식을 보겠습니다.

\[ \displaystyle J(\theta) = \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^2 + \sum_{i=1}^{n}\vert\theta_{i}\vert \]

이렇게 \(\theta\) 값들의 절댒값을 손실 함수에 모두 더해주면 됩니다.
그런데 이 때, \(\theta_{0}\)은 과적합과 상관이 없기 때문에 \(\theta_{0}\)은 더해주지 않습니다.

그런데 실제로는 정규화 항에 \(\lambda\)도 곱해주는데, \(\theta\)값이 커지는 것에 대해 얼마나 페널티를 줄지를 정해주는 것입니다.

\[ \displaystyle J(\theta) = \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^2 + \lambda\sum_{i=1}^{n}\vert\theta_{i}\vert \]

예를 들어 \(\lambda\)값이 크면 \(\theta\)값들이 조금만 커져도 손실 함수가 굉장히 커지므로 \(\theta\)를 줄이는 게 우선이고,
\(\lambda\)값이 작으면 \(\theta\)값이 커져도 손실 함수가 별로 안커지므로 MSE를 줄이는 것이 우선입니다.

L1 정규화를 적용하는 회귀 모델을 Lasso Regression 또는 Lasso model 이라고 얘기합니다.

L2 정규화

L2 정규화도 L1 정규화와 거의 유사한데 \(\vert\theta\vert\)값들을 모두 더하는 대신에 \(\theta^{2}\)의 값들을 모두 더해주면 됩니다.

\[ \displaystyle J(\theta) = \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^2 + \lambda\sum_{i=1}^{n}\theta_{i}^{2} \]

L2 정규화를 적용하는 회귀 모델을 Ridge Regression 또는 Ridge model 이라고 얘기합니다.

scikit-learn으로 과대적합 방지해보기

L1, L2 정규화 일반화

위에서는 계속 예시로 다항 회귀 모델을 사용했는데,
다른 모델들에도 정규화는 똑같이 적용할 수 있습니다.

앞서 다뤘던 모델들을 대상으로는
LinearRegression 대신 Lasso나 Ridge를 쓰면 되고,
LogisticRegression에는 penalty라는 옵셔널 파라미터를 전달해주면 됩니다. 참고 링크

나중에 다룰 딥러닝 모델도 손실 함수를 최소화하는 알고리즘입니다.
딥러닝 모델도 과적합되는 경우가 많아서 딥러닝 할 때에도 정규화는 중요합니다.

딥러닝 모델의 파라미터는 보통 \(\theta\)대신 \(w\)로 나타냅니다.
딥러닝 모델에 정규화를 적용하려면 모델의 손실 함수에 정규화 항으로 아래 둘 중 하나를 더해주면 됩니다.

\[ \displaystyle \lambda\sum_{i=1}^{n}\vert w_{i} \vert, \lambda\sum_{i=1}^{n}w_{i}^{2} \]

L1, L2 정규화의 차이

L1 정규화는 여러 \(\theta\)값들을 0으로 만듭니다. 모델에 중요하지 않다고 생각되는 속성을 없애는 역할을 합니다.
L2 정규화는 \(\theta\)값들을 0으로 만들기보다는 조금씩 줄여줍니다. 모델에 사용되는 속성을 없애지는 않습니다.
(이렇게 되는 이유가 궁금하다면 여기를 참고하세요)

L1 정규화는 어떤 모델에 쓰이는 속성 또는 변수의 개수를 줄이고 싶을 때 사용합니다.
속성이 너무 많으면 과적합 뿐만이 아니라 모델을 학습시킬 때 많은 자원을 소모할 수 있습니다.
이럴 때 L1 정규화를 사용하면 사용되는 속성의 개수를 많이 줄일 수 있습니다.

반대로 딱히 속성의 개수를 줄일 필요가 없다고 생각되면 L2 정규화를 사용하면 됩니다.